Arithmetic Aptitude - Pythagorean Theorem

Arithmetic Aptitude - Pythagorean Theorem questions with answers

<-- Back to Percentages

Next to Time Travel -->

If the area of square A is 169 m² and the area of square B is 144 m², what will be the perimeter of square C?
1. 25 m
2. 5 m
3. 36 m
4. 20 m
View Answer

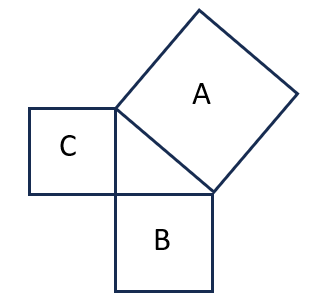
Answer: D. 20 m

Explanation:
The triangle PQR formed by the three squares is a right-angled triangle (right-angled at Q). Hence, using Pythagorean theorem, PR²= PQ² + QR²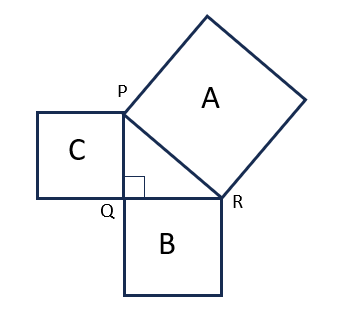
Here, PR² represents the area of square A and QR² represents the area of square B. Therefore, 169 = PQ² + 144
So, PQ² = 25, which is the area of square C.
Also, hence, PQ = 5 m which represents a side of square C.
Finally, the perimeter of square C will be 4 X 5 = 20 m.

A chess board is made of 8X8 square boxes. Each square box is 3 cm in length. What will be the length of the diagonal across the entire chess board?
1. 27.8 cm
2. 36.66 cm
3. 576 cm
4. 33.94 cm
View Answer

Answer: D. 33.94 cm

Explanation:
Consider the chess board as shown in the figure. Each side of the chess board will measure = 8 X 3 = 24 cm.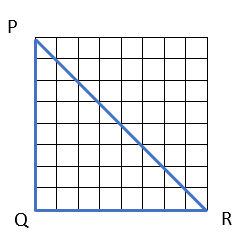
Additionally, angle at Q is right-angled and triangle PQR forms a right-angled triangle.
Therefore, using Pythagorean Theorem,
PR² = PQ² + QR²
PR² = 24² + 24²
PR² = 576 + 576 = 1152
PR = 33.94 cm, which is the length of the diagonal of the chess board.
Find the perimeter of a rhombus whose diagonals are 16 cm and 8 cm in length?
Note: The diagonals of a rhombus are perpendicular to each other and bisect each other.
1. 8.94 cm
2. 17.88 cm
3. 71.55 cm
4. 35.76 cm
View Answer

Answer: D. 35.76 cm

Explanation:
Since the diagonals of a rhombus are perpendicular and bisect each other, hence, in triangle POT, angle O is right-angled triangle. Also, PO = 4cm and OT = 8cm.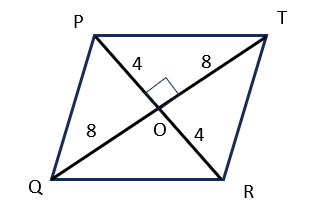
Therefore, using Pythagorean theorem,
PT² = PO² + OT²
PT² = 4² + 8² = 16 + 64 = 80
PT = 8.94 cm
Perimeter of rhombus = 4 * side = 4 * 8.97 = 35.76 cm
A child is standing 30 feet away from a light house which is 25 feet in height. A flag pole is placed on top pf the light house. Use the figure given below to calculate the height of the flag pole.
1. 8.54 feet
2. 37.41 feet
3. 33.54 feet
4. 18.4 feet
View Answer

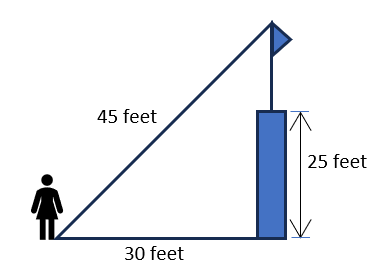
Answer: A. 8.54 feet

Explanation:
Triangle ABC is right-angled at B.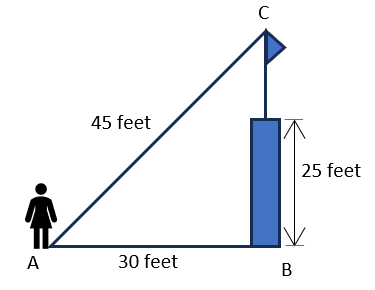
Using Pythagorean Theorem,
AC² = AB² + BC²
BC² = AC² – AB²
BC² = 45² – 30²
BC² = 2025 – 900 = 1125
BC = 33.54 feet
Height of flag pole = 33.54 – height of light house
= 33.54 – 25 = 8.54 feet
Andy bought a new table top as shown in figure below. Next morning when he woke up, he saw a grass-hopper sitting on one end of the table diagonal and a caterpillar on the other. If the grass-hopper walks at a speed of 0.5 inches/sec, how long will it take for the it to reach the caterpillar?
1. 83.56 sec
2. 86.56 sec
3. 86.53 sec
4. 83.53 sec
View Answer

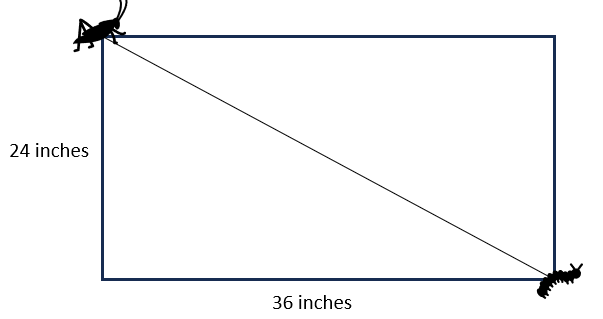
Answer: C. 86.53 sec

Explanation: We first need to find the distance between grass-hopper and the caterpillar.

Triangle ABC is right-angled at B.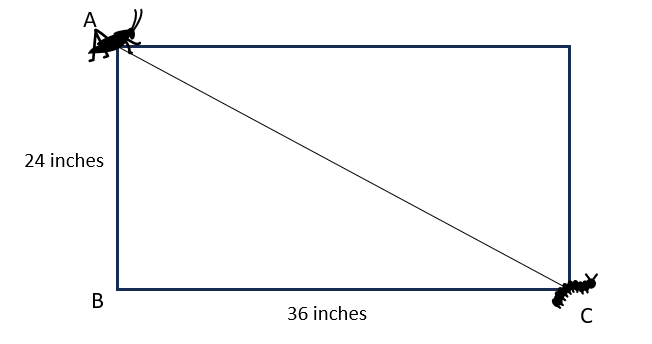
Using Pythagorean Theorem,
AC² = AB² + BC²
AC² = 24² + 36²
AC² = 576 + 1296
AC² = 1872
AC = 43.26 inches
Speed of grass-hopper is 0.5 inches/sec
Therefore,

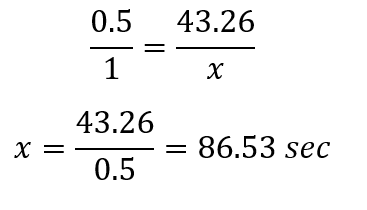
Andrew and Sandy ran across the diagonals of the two parks as shown in the figure. Who of the two ran longer distance and by how much?
1. Andrew ran 4 m more than Sandy
2. Andrew and Sandy both ran almost the same distance
3. Andrew ran 2 m more than Sandy
4. Sandy ran 2 m more than Andrew
View Answer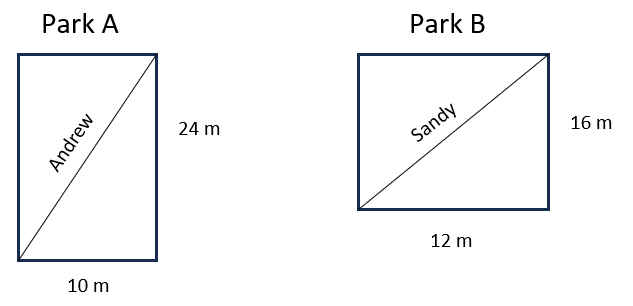

Answer: B. Andrew and Sandy both ran almost the same distance

Explanation:
Distance ran by Andrew can be found by calculating the length of the diagonal of park A. In Park A, triangle ABC is right-angled at B. Therefore, using Pythagorean Theorem,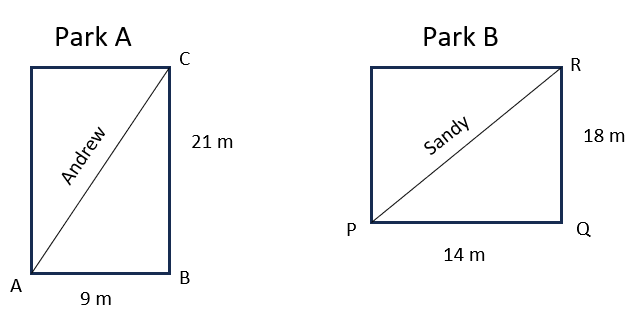
AC² = AB² + BC²
AC² = 9² + 21²
AC² = 81 + 441
AC² = 522
AC = 22.84 m
Now, distance ran by Sandy can be found by calculating the length of the diagonal of park B. In Park B, triangle PQR is right-angled at Q. Therefore, using Pythagorean Theorem,
PR² = PQ² + QR²
PR² = 14² + 18²
PR² = 196 + 324
PR² = 520
PR = 22.80 m

Maria is using a ladder to clean the top-most window of a tall building (as shown in the figure). The length of her ladder is 22 feet. There is a garden right next to the building because of which Maria can only place the ladder at 10 feet from the building. The window is at a height of 24 feet from the ground. Will she be able to reach the window?
1. Maria will not be able to reach the window with the ladder she has. She needs a ladder which is at least 26 feet in length
2. Maria will not be able to reach the window with the ladder she has. She needs a ladder which is at least 24 feet in length
3. Maria will not be able to reach the window with the ladder she has. She needs a ladder which is at least 676 feet in length
4. Maria will be able to reach the window with the ladder she has
View Answer

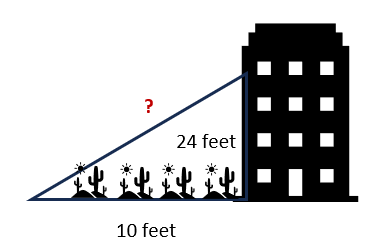
Answer: A. Maria will not be able to reach the window with the ladder she has. She needs a ladder which is at least 26 feet in length

Explanation: We need to calculate the minimum length of the ladder required.
Triangle ABC is right- angled at B. Using Pythagorean Theorem,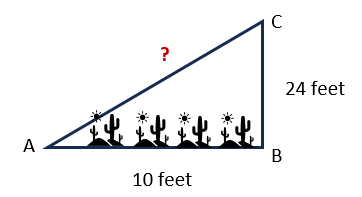
AC² = AB² + BC²
AC² = 10² + 24²
AC² = 100 + 576
AC² = 676
AC = 26 feet
Therefore, Maria needs ladder which is minimum 26 feet in length to reach the window.

Sam started swimming across a 12 feet wide river. The upward current drifted him 9 feet away (upwards) from the original position (started swimming from point A and reached point B). What is the actual distance that Sam swim?
1. The actual distance that Sam swim is 25 feet
2. The actual distance that Sam swim is 10 feet
3. The actual distance that Sam swim is 15 feet
4. The actual distance that Sam swim is 12 feet
View Answer

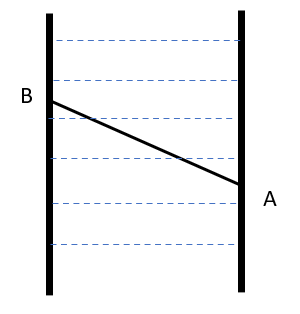
Answer: C. The actual distance that Sam swim is 15 feet

Explanation:
As shown in the figure, Sam started to swim at point A and reached point B across the river. He was drifted by 9 feet because of the upward current. Therefore, BC = 9 feet.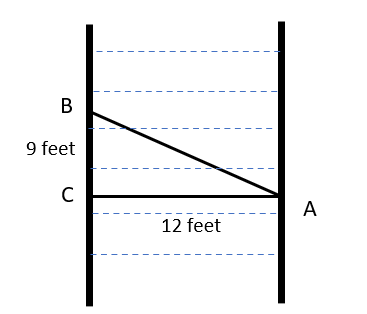
Also, given that the width of the river is 12 feet. Hence, AC = 12 feet
Moreover, triangle ABC is right-angled triangle, right-angled at C.
Using Pythagorean Theorem,
AB² = BC² + AC²
AB² = 9² + 12²
AB² = 81 + 144
AB² = 225
AB = 15 feet

In a hospital, a ramp is to be constructed for wheelchair riders to reach a floor which is 5 feet in height. The ramp should start 11 feet away from the foot of the floor. What will be the length of the ramp?
1. The length of the ramp should be 14.04 feet
2. The length of the ramp should be 6.04 feet
3. The length of the ramp should be 24.16 feet
4. The length of the ramp should be 12.08 feet
View Answer

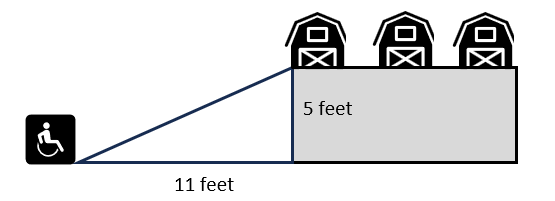
Answer: D. The length of the ramp should be 12.08 feet

Explanation:
As shown in the figure, to calculate the length of the ramp, we need to calculate the length of AC. Triangle ABC is right-angled at B. Using Pythagorean Theorem,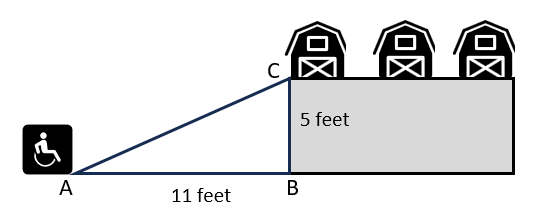
AC² = AB² + BC²
AC² = 11² + 5²
AC² = 121 + 25
AC² = 146
AC = 12.08 feet

Two planes started from the airport and flew in different directions as shown in the figure.

What will be the distance between the two planes, when their individual distances from the airports are 28000 kms and 45000 kms respectively?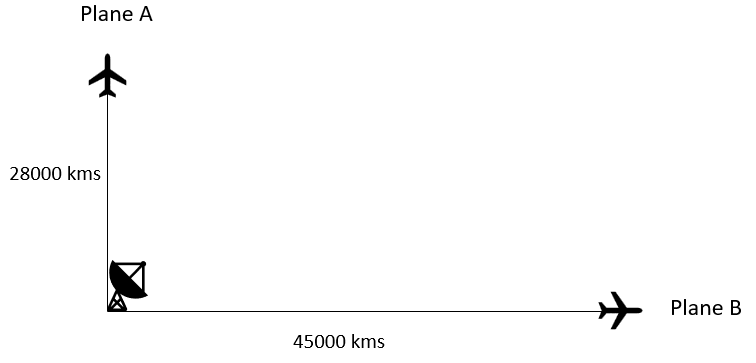
1. The individual distances between the planes will be 53000 kms
2. The individual distances between the planes will be 53300 kms
3. The individual distances between the planes will be 35500 kms
4. The individual distances between the planes will be 35000 kms
View Answer

Answer: A. The individual distances between the planes will be 53000 kms

Explanation:

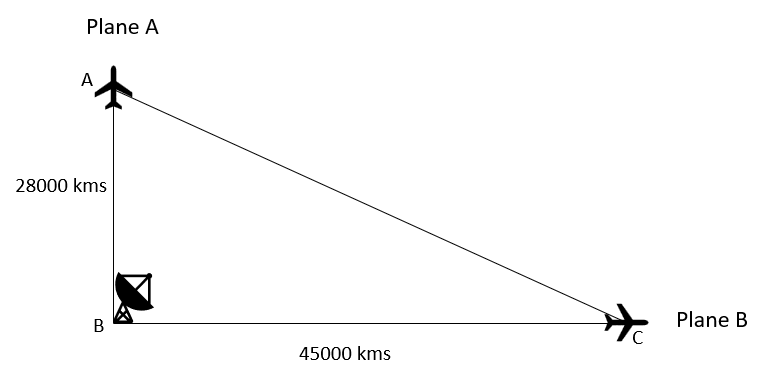
Let us assume that the two planes form a triangle ABC as shown in the figure below. This triangle is right-angled at B. The distance between the two planes will be the measure of line segment AC.
Using Pythagorean Theorem,
AC² = AB² + BC²
AC² = (28000)² + (45000)²
AC² = 784000000 + 2025000000
AC² = 2809000000
AC = 53000 kms

<-- Back to Percentages

Next to Time Travel -->